Geometric Operators

Geometric Modeler	Geometry	Geometric Operators The general use explained on an example
Use Case

Abstract

Geometric operators are transient objects that allow you to create new geometric objects from existing ones or to analyze them. These operators are based on the same scheme, which is described. The example of the intersection between a curve and a surface illustrates the general mechanism, and is discussed using the CAAGopIntersect.cpp sample.

What You Will Learn With This Use Case
The Geometric Operators
How to Use a Geometric Operator
The CAAGopIntersect Use Case
Step-by-Step
In Short
References

What You Will Learn With This Use Case

This use case is intended to help you use the geometric operator classes. It particularly details the intersection geometric operator, as an example of geometric operator.

[Top]

The Geometric Operators

Using geometric operators is an easy way to create or analyze geometric objects. While the geometric objects provide basic services, that are easily computed by the objects themselves, the geometric operators do more complex operations using advanced mathematics tools. As an example, evaluations from parameters to Cartesian coordinates is offered by the geometric curve or surface, whereas the torsion or curvature are computed by a geometric operator.

All these operators never modify the input objects: they create new ones.

The geometric operators work inside one geometric container: the input and output objects must belong to the same geometric container.

The operators creating geometric objects are:

Intersection between
- Two curves (CATIntersectionCrvCrv)
- Two surfaces (CATIntersectionSurSur)
- A curve and a surface (CATIntersectionCrvSur)
Projection of
- A curve on a surface (CATProjectionCrvSur)
- A point on a curve (CATProjectionPtCrv) or a surface (CATProjectionPtSur)
Creation of reflect lines (CATReflectCurve
Creation of edge curves (CATEdgeCurveComputation).

The operators of geometric analysis are:

Confusion of
- Two points of a curve (CATConfusionPtOnCrvPtOnCrv)
- Two points of a surface (CATConfusionPtOnSurPtOnSur)
Inclusion of
- A point on a curve (CATInclusionPtCrv)
- A point on a surface (CATInclusionPtSur)
Minimum distance between
- Two curves (CATDistanceMinCrvCrv),
- A point and a curve (CATDistanceMinPtCrv)
- A point and a surface (CATDistanceMinPtSur)
Local analysis of a point on a curve (CATLocalAnalysis1D), or a surface (CATLocalAnalysis2D)
Global analysis of a point a a curve (CATMassProperties1D).

The geometric operators are generic: the CATIntersectionCrvSur operator, for example, computes the intersection of any type of curves with any type of surfaces.

[Top]

How to Use a Geometric Operator

All the geometric operators are based on the same scheme. The geometric operator instances, created by a global function, are transient (that is to say, they are not streamed when streaming the geometric factory). They are used to declare an operation, to run it, and to retrieve the resulting objects.

The geometric operators can be used in two modes, BASIC or ADVANCED.

In the BASIC mode, data given when creating the operator is sufficient to execute it, and the operation is automatically run.
In the ADVANCED mode, the operator can be tuned after its creation with advanced options. You have then to explicitly ask for its execution. In any cases, the resulting objects are not created during the execution step. They are created when you ask for them, by calling the GetXxx methods. These methods are often presented as iterators:
- A method to retrieve the number of solutions
- An initialization of the iterator
- A method to increment the iterator
- A method to retrieve (and, hence create) the geometric result.

For example, the intersection between a curve and a surface can lead to several resulting points and curves, so that this operator provides iterators on the resulting points and on the resulting curves.

[Top]

The CAAGopIntersect Use Case

CAAGopIntersect is a use case of the CAAGeometricOperators.edu framework that illustrates GeometricOperators framework capabilities.

[Top]

What Does CAAGopIntersect Do

Fig. 1: The Geometry of the CAAGopIntersect Use Case
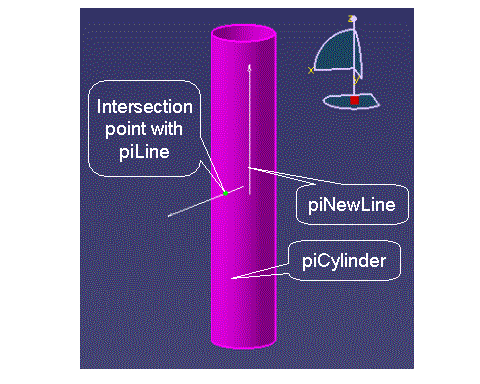
	This use case presents the global scheme of the geometric operators and takes the curve-surface intersection operator as example. The curve is a line, and the surface a cylinder. The operator being independent of the type of curve or surface, any kind of curve or surface can be used in the same way.

[Top]

How to Launch CAAGopIntersect

To launch CAAGobIntersect, you will need to set up the build time environment, then compile CAAGobIntersect.m along with its prerequisites, set up the run time environment, and then execute the use case [4].

If you simply type CAAGopIntersect with no argument, the use case executes, but doesn't save the result in an NCGM file. If you want to save this result, provide the full pathname of the NCGM file to create. For example:

With Windows CAAGopIntersect e:\Intersect.NCGM

With UNIX CAAGopIntersect /u/Intersect.NCGM

This NCGM file can be displayed using the CAAGemBrowser use case.

[Top]

Where to Find the CAAGopIntersect Code

The CAAGopIntersect use case is made of a main named CAAGopIntersect.cpp located in the CAAGopIntersect.m module of the CAAGeometricOperators.edu framework:

Windows	`InstallRootDirectory\CAAGeometricOperators.edu\CAAGopIntersect.m\`
Unix	`InstallRootDirectory/CAAGeometricOperators.edu/CAAGopIntersect.m/`

where InstallRootDirectory is the directory where the CAA CD-ROM is installed.

[Top]

Step-by-Step

CAAGopIntersect.cpp is divided into five logical steps:

Creating the Geometry Factory
Creating the Line and Cylinder to Intersect
Using the BASIC Mode

Creating the operator
Getting the results by using the iterators
Deleting the operator

Using the ADVANCED Mode

Creating the operator
Running
Getting the results
Modifying input parameters
Running again
Deleting the operator.

Writing the Model And Closing the Container

[Top]

Creating the Geometry Factory

The geometry factory (CATGeoFactory) creates and manages all the CATICGMObject (and the curves and surfaces in particular) [1]. This creation is done by the global function ::CATCreateCGMContainer. Notice that the factory can be defined by reading a NCGM file that was previously stored. In that case, the global function ::CATLoadCGMContainer must be used.

CATGeoFactory* piGeomFactory = ::CATCreateCGMContainer() ;
if (NULL==piGeomFactory) return (1);

[Top]

Creating the Line and Cylinder to Intersect

// ------------ line passing thru (0,0,0), of direction (1.,1.,0)
CATLine * piLine = piGeomFactory->CreateLine(CATMathO,     // (0,0,0) math point
                                             CATMathVector(1.,1.,0.) );
if (NULL==piLine) 
{
  ::CATCloseCGMContainer(piGeomFactory);
  return (1);
}
//
// ------------ cylinder 
double radius = 10.;
double axisStart = -50.;
double axisEnd = 50.;
double angleStart = 0.;
double angleEnd = CAT2PI;
CATCylinder* piCylinder = piGeomFactory->CreateCylinder(CATMathOIJK, // canonical axis system
                                                        radius,
                                                        axisStart,
                                                        axisEnd,
                                                        angleStart,
                                                        angleEnd);
if (NULL==piCylinder) 
{
  ::CATCloseCGMContainer(piGeomFactory);
  return (1);
}

The geometry is created by the CATGeoFactory with the CreateLine and CreateCylinder methods.

[Top]

Using the BASIC Mode

To operate in this mode, write the following steps:

Creates the operator with the appropriate global function (CreateIntersection), and specify the BASIC mode (or without specifying any mode: by default, the operator is created with the BASIC mode). The global function executes the requested operation and returns the corresponding operator instance.
Gets the result with the desired iterator, here a point iterator:
- Retrieves the number of solution points: GetNumberOfPoints
- Skips to the next point: NextPoint
- Creates the current geometric point: GetCartesianPoint
Deletes the operator instance.

//  creation and run
CATIntersectionCrvSur* pIntOp = ::CreateIntersection(
                       piGeomFactory,   // geometric factory 
                       piLine,          // geometric line
                       piCylinder,      // geometric cylinder
                       BASIC);          // the mode (default value)
//
// get the results
if (NULL == pIntOp) return (3);
long nbPoints = pIntOp->GetNumberOfPoints();

cout << "Basic case: Number of intersection points: "<< nbPoints 
     << endl;
if (0 != nbPoints) 
{
  // iterator on the resulting points
  pIntOp->BeginningPoint();	         // initialization
  while(TRUE== (pIntOp->NextPoint()) )   // loop on the resulting points
  {
    // create the geometric point
    CATCartesianPoint* piPoint=pIntOp->GetCartesianPoint(); 
    double x,y,z;
    if (NULL != piPoint)
    {
      piPoint->GetCoord(x,y,z);
      cout << " X= "<< x << " Y= "<< y << " Z= "<< z <<endl;
      // remove the point if you do not want to keep it
      piGeomFactory->Remove(piPoint); 
    }                          
  }
}
// delete the operator
delete pIntOp; 
pIntOp = NULL;

The BASIC mode is the default mode. This argument can be omitted

The CATICGMContainer::Remove method removes the point from the geometry factory. If the point is not removed, it is streamed when streaming the factory.

Note: Although geometric objects are handled by the mean of interfaces, such as CATCartesianPoint, CATLine, or CATBody, the pointers on these objects must not be released. In fact, they are released at the closure of the factory (the CATCloseCGMContainer global function).

[Top]

Using the ADVANCED Mode

This mode can be use, in case of the curve - surface intersection:

To set advanced parameters: the limits on the geometry to take into account for this operation
To run again the operator on a different curve. This mode can be useful where performing intersections between a surface and a bunch of curves.

To operate in this mode, write the following steps that:

Create the operator with the appropriate global function (CreateIntersection), and specify the ADVANCED mode. The global function returns the corresponding operator instance, but does not run the operation
Specify additional information or advanced options to the operator by calling one of its SetXxx methods: for example here SetLimits
Execute the operation: Run method
Get the result with the desired iterator
Optionally, set new options, run again the operator, and retrieve the new results
Remove the operator instance from the memory.

CATIntersectionCrvSur* pIntOp = ::CreateIntersection(
                                piGeomFactory,    // geometric factory
                                piLine,           // geometric line
                                piCylinder,       // geometric cylinder
                                ADVANCED);        // MODE
if (NULL==pIntOp) return (3);

// set  limits. These limits were previously defined or computed
pIntOp->SetLimits(crvLimits);

// run
pIntOp->Run();

// get the results
// ... same way as in BASIC mode ..., but not same result! 
// as the curve limits are more restrictive, only one solution is found

// set another line and new limits

pIntOp->SetCurve(piNewLine);     // piNewLine was previously created
pIntOp->SetLimits(newCrvLimits); // newCrvLimits was previously defined

// run again 
pIntOp->Run();

// get the results
nbPoints = pIntOp->GetNumberOfPoints();
cout << " Number of intersection points: "<< nbPoints << endl;
long nbCurves= pIntOp->GetNumberOfCurves();
cout << "Number of intersection curves: "<< nbCurves << endl;

// delete
delete pIntOp;  
pIntOp=NULL;

Note:

If you only ask for the number of solutions, without getting the corresponding geometric objects, these objects are not created in the geometric factory. So you will not see them at the visualization of the NCGM document. In the use case, the NewLine curve is lying on the cylinder. There is a curve solution, that is not created, because the GetPCurve method is not called.
The limits are defined by two CATCrvParam. These CATCrvParam are directly computed by calling the CATCurve::GetParam method on two cartesian points. This is only possible, first because these points belong to the curve, and second because the line is a canonical entity. In other cases, you must use CATProjectionPtCrv to retrieve the CATCrvParam corresponding to a CATPoint on a given curve.

CATCrvParam  startParam, endParam;

// piLine is the line of origin CATMathO and of direction (1.,1.,0.)
// The use of GetParam is only possible because the points belong to the line
// and piLine is canonical.
// In other cases use a CATProjectionPtCrv operator
piLine->GetParam(CATMathO,startParam); 

// another point on the line      
piLine->GetParam(CATMathPoint(35.,35.,0.),endParam);

// the limits
CATCrvLimits crvLimits(startParam,endParam);

[Top]

Writing the Model and Closing the Factory

To save the model in a file, the ::CATSaveCGMContainer global function is used. Notice that in the use case, the save is conditioned by an input parameter representing the file inside which the model must be saved.

The use case ends with the closure of the geometry factory, done by the ::CATCloseCGMContainer global function.

 if(1==toStore)
 {
#ifdef _WINDOWS_SOURCE
   ofstream filetowrite(pfileName, ios::binary ) ;
#else
   ofstream filetowrite(pfileName,ios::out,filebuf::openprot) ;
#endif

   ::CATSaveCGMContainer(piGeomFactory,filetowrite);
   filetowrite.close();
 }	

 //
 // Closes the container
 //	
 ::CATCloseCGMContainer(piGeomFactory);

[Top]

In Short

The geometric operators are transient objects used to create or analyze geometric objects. They do not modify the input operands.
All the geometric operators are based on the same scheme: creation, optionally set of advanced options, run, read of the results, deletion. They work inside one container.

[Top]

References

[1]	The CGM Objects
[2]	The CGM Curves
[3]	The CGM Surfaces
[4]	Building and Launching a CAA V5 Use Case
[Top]

History

Version: 1 [Feb 2000]	Document created
[Top]

Geometric Modeler

Geometry