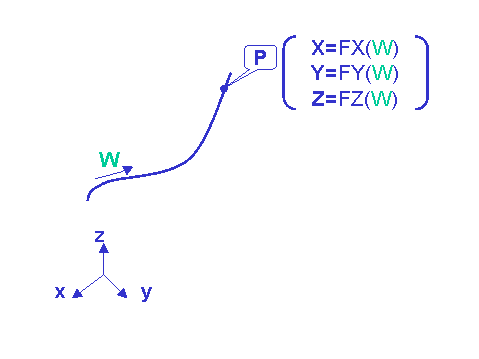
Geometric Modeler

Introduction

A curve is a function from a closed interval of R to R^3. Hence, it is defined by three scalar functions of one variable. The variable is usually called parameter of a point on the curve and denoted through W, while the scalar functions represent the mapping, for each point of the curve, between the Cartesian coordinates, usually called X, Y, Z, and the corresponding parameter W.

Fig. 1: The mapping between the parameter and the Cartesian coordinates

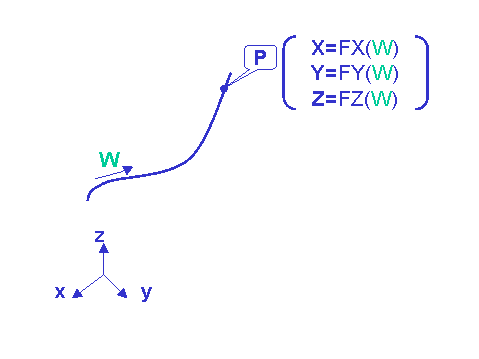Three scalar functions FX, FY and FZ map the W parameter into the Cartesian coordinates (X, Y, Z) for each point P of the curve.

Multi-arcs curves are defined as a set of n_w connected pieces, each piece, called arc, having its own parameterization. Hence, a point belonging to the curve can be expressed in terms of:

• Local parameters: w parameter on a given arc, independently of the other arcs
• Global parameters: W parameter taking into account the preceeding arcs parameterization.

Fig. 1b: Local and global parameters on a 2 arcs curve

The Cartesian coordinates of the point P can be evaluated using the global parameter W, or the local parameter w_2 on the 2nd arc.

[Top]

Properties of the CGM Curves

The CGM curves implement the CATCurve interface, which behavior is now described. The CATCurve interface inherits all the behavior of the CATGeometry interface. Therefore, the factory of the CGM objects (CATGeoFactory) handles the creation, stream, unstream and remove of the CGM curves. The geometric transformation and/or duplication of CGM curves is managed by specific processes through CATTransfoManager and CATCloneManager instances [3]. For more details about the CGM objects general properties, see [1].

[Top]

Validity Criteria

1. CGM curves must be C2 continuous. Hence, the curves are many infinitely differentiable with respect to the W parameter on each arc, and only twice continuously differentiable between two arcs. CGM directly generates objects satisfying this criterion. If you want to introduce foreign curves, you have to insure that they satisfy it. If they do not satisfy it, you can cut them where they are not C2 continuous, and use topological objects to assemble the parts.

   Fig. 2: Valid (C) and invalid (A, B) curves

   In addition, the curves must not be self intersecting, except if they are closed curves.

2. Finally, the curvilinear length must be greater than the resolution of the factory. The resolution defines the minimum length of a valid object, see [1].
3. The derivatives at a point within the curve must not be null. This condition implies that you have no cusps.
4. The derivatives at the curve extremities must neither be null (strongly recommended).
5. The curvature radius at any point of the curve must be greater that the resolution.
6. Each curve arc must have a length greater than the resolution.
7. The parametrization must be as close as possible to the curvilign (3D tangent norm between 0.1 and 10).

Specific objects

1. Canonical objects such as circles and ellipses must be included in the geometric infinite.
2. CATEllipses and CATPEllipses: the ratio between min radius and max radius must be greater than resolution.
3. NURBS: the distance between two control points must be greater than the resolution.
4. PCurves: the maximum limits of a PCurve must stay within the maximum limits of its support.

[Top]

Class for Handling Curve Parameter

The curve parameter only has sense if it is associated with the curve it parameterizes. This parameter is handled through a CATCrvParam instance, which is a transient object containing the parameter and a reference to the curve. In particular, it transforms a global parameter into a local parameter and an arc, and vice versa. The CATCrvParamReference transient instance can not directly be created; the curve is responsible for retrieving a CATCrvParam instance under your request.

[Top]

Limits and Bounding Box of a Curve

A curve has a maximal limitation, outside which it is not defined, or cannot be extrapolated. This limitation is expressed in terms of a CATCrvLimits transient instance, containing two CATCrvParam instances.

Geometric operators can be run on a part of the whole curve, therefore defining a current limitation. This current limitation is also handled by the CATCrvLimit class.

Each curve is able to retrieve the definition of a space that surrounds it: the bounding box. This information is very useful, especially if you want to have a first diagnostic of intersection for example.
The bounding box contains two points, and can be a CATMathBox instance, if expressed with Cartesian coordinates, or a CATCrvParam instance, if expressed with the curve parameter.

[Top]

Evaluation

The main behavior of a curve is to evaluate the Cartesian coordinates from the parameter of a point lying on it and, conversely, the parameter from Cartesian coordinates:

• From the parameter to Cartesian coordinates. This is called evaluation (CATCurve::Eval), and is done to obtain the Cartesian coordinates of the point, or the vector of the curve derivatives at a given point. Multiple evaluation can be used to save CPU by the means of a CATCrvEvalCommand instance.
• From Cartesian coordinates to the parameter. The CATCurve::GetParam method computes (if possible) the curve parameter of a given Cartesian point, and details if the point really is on the curve or not, and if there are several solutions.

The curve is responsible for the mapping between the (X, Y, Z) Cartesian coordinates and the W parameter, so that no assumptions must be maid about this mapping, except for a few objects that have published their own parameterization.

[Top]

Equations

It is useful to retrieve the equations representing the curve, especially when you want to operate the geometry. You can retrieve these equations as CATMathFunctionXY instances, that are transient and created under request.

All curve modification changes the equations. Thus, it is necessary to precisely define the use of the geometry equations. There are 3 main methods for using equations.

• CATCurve::Lock(): Locks the geometric object before asking for its equation. This operation:
• Declares a reference on the object, so that it cannot be deleted anymore.
• Increments the number of customers that wants to prevent the object from future modifications, except the relimitation.
• Does not compute anything.
• CATCurve::GetEquation(): Asks for the equation. This operation:
• Throws an exception if the object is not locked.
• Allocate the memory (if needed).
• Computes the equations (if needed).
• Returns a constant pointer to the required equation.
• CATCurve::Unlock(): Unlocks the geometric object when you do not need to use its equation no more. This operation:
• Releases the reference
• Decrements the number of customers which want to prevent the object from future modifications, except the relimitation.
• Keeps the allocated memory and computed equations as long as the object is not modified.

In case of a curve modification,

• If there remains at least one lock on the curve, an error is thrown
• Otherwise, the memory is freed.

[Top]

Various Types of Curves

You find three major curve types in the CGM offering: the resolved curves, the edge curves, the PCurves. You can also introduce your own class of curve, and use it as any CGM curve in all the CGM operators or as the underlying geometry of a topological object. For a detailed description of this mechanism, see [2].

[Top]

Resolved Curves

These curves have a mathematical form: line, conic (circle, ellipse, parabola, hyperbola), NURBS, Spline belong to this type. Evaluations are made directly from the mathematical equations. The following array describes, for each resolved curve, its definition parameters, and the validity range of the definition parameters which come in addition to general validity criteria that have already been described.

[Top]

Edge Curves

An edge curve is the geometric curve, that can be seen under several representation. [4] describes in details this geometric curve. It is in particular used to define the geometry of a topological edge.

[Top]

PCurves

These geometric objects are used to define curves in the parameter space of a surface. For example, a PLline is a curve which mathematical representation in the space of the surface is a line. Hence, in the 3D space, this object can be a line, a circle, or a much more complex curve, if it lays on a CATNurbs surface for example.

Additional methods are available on PCurves: the equations, the derivatives and the boundng box can be retrieved in the (U,V) space of the underlying surface.

figures

All the resolved curves are available as PCurves on any type of CGM surfaces.

[Top]

In Short

• CGM curves are C2 continuous. They offer you evaluators to evaluate point parameters and derivatives, and equations to use in geometric operations for example.
• Three major types of curves are available: resolved curves, edge curves and PCurves. Foreign curves can also be introduced in CGM.

[Top]

References

History

Copyright © 2000, Dassault Systèmes. All rights reserved.