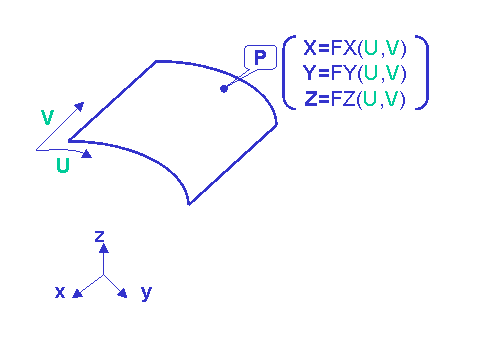
Geometric Modeler

Introduction

A surface is a function from a closed interval of R^2 to R^3. Hence, it is defined by three scalar functions of two variables. The variables are usually called parameters of a point on the surface and denoted through U and V, while the scalar functions represent the mapping, for each point of the surface, between the Cartesian coordinates, usually called X, Y, Z, and the corresponding parameters U and V.

Fig. 1: The mapping between the parameters and the Cartesian coordinates

Three scalar functions FX, FY and FZ map the (U,V) parameters into the Cartesian coordinates (X, Y, Z) for each point P of the surface.

Multi-patches surfaces are defined as a set of (n_u*n_v) connected pieces, each piece, called patch, having its own parameterization. Hence, a point belonging to the surface can be expressed in terms of:

• Local parameters: (u,v) parameters on a given patch, independently of the other patches
• Global parameters: (U,V) parameters taking into account the preceding patches parameterization.

Fig. 1b: Local and global parameters on a 3*2 patches surface

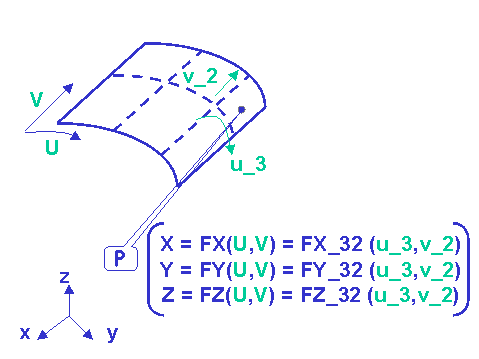The Cartesian coordinates of the point P can be evaluated using the global parameter (U,V), or the local parameter (u_3,v_2) on the (3,2)th patch.

[Top]

Properties of the CGM Surfaces

The CGM surfaces implement the CATSurface interface, which behavior is now described. The CATSurface interface inherits all the behavior of the CATGeometry interface. Therefore, the factory of the CGM objects (CATGeoFactory) handles the creation, stream, unstream and remove of the CGM surfaces. The geometric transformation and/or duplication of CGM surfaces is managed by specific processes through CATTransfoManager and CATCloneManager instances [3]. For more details about the CGM objects general properties, see [1].

[Top]

General Validity Criteria

1. CGM surfaces must be C2 continuous. Hence, the surfaces are many infinitely differentiable with respect to the (U,V) parameters on each patch, and only twice continuously differentiable between two patches. CGM directly generates objects satisfying this criterion. If you want to introduce foreign surfaces, you have to insure that they satisfy it. If they do not satisfy it, you can cut them where they are not C2 continuous, and use topological objects to assemble the parts.

   Fig. 2: Validity criteria for surfaces

   In addition, the surfaces must not be self intersecting, except if they are closed (as for a cylinder for example). On the other hand, they can be degenerated, but only on one or two boundaries that are not adjacent.

2. In each direction, (U and V), the curvilinear length must be greater than the resolution of the factory. The resolution defines the minimum length of a valid object, see [1].
3. The normal to the surface must not be null (except possibly at a point on the surface boundary). This applies to degenerate isoparametric curves.
4. The normal can only be null on a degenerate boundary (of a sliver face for example).
5. The surface curvature radius must be greater than the resolution.
6. Each patch must have a 3D length greater than the resolution  along U and V.
7. The surface parametrization must be as close as possible to the curvilign (the norm of the partial derivatives must be around 1 and always in the 0.1-10 range).

Specific objects

1. Nurbs Surfaces: control points should be in the geometric infinite
2. Nurbs Surfaces: control points should be distant from more than the resolution
3. Nurbs Surfaces: degree must be less than 15

[Top]

Class for Handling Surface Parameters

The surface parameters only have sense if they are associated with the surface they parameterize. These parameters are handled through the CATSurParam instances, which are transient objects containing the parameters in each directions and a reference to the surface. In peculiar, they transform global parameters into local parameters and patches, and vice versa. The CATSurParamReference transient instance can not directly be created; the surface is responsible for retrieving a CATSurParam instance under your request.

[Top]

Limits and Bounding Box of a Surface

A surface has a maximal limitation, outside which it is not defined, or cannot be extrapolated. This limitation is expressed in terms of a CATSurLimits transient instance, containing two CATSurParam instances.

Geometric operators can be run on a part of the whole surface, therefore defining a current limitation. This current limitation is also handled by the CATSurLimit class.

Each surface is able to retrieve the definition of a space that surrounds it: the bounding box. This information is very useful, especially if you want to have a first diagnostic of intersection for example.
The bounding box contains two points, and can be a CATMathBox instance, if expressed with Cartesian coordinates, or a a CATSurParam instance, if expressed with parameters.

[Top]

Evaluation

The main behavior of a surface, for a point lying on this surface, is to evaluate the Cartesian coordinates from its parameters and, conversely, the parameters from Cartesian coordinates:

• From parameters to Cartesian coordinates. This is called evaluation, and can be done to obtain the Cartesian coordinates of the point, or the vector of the surface derivatives at a given point. Multiple evaluation can be used to save CPU by the means of a CATSurEvalCommand instance.
• From Cartesian coordinates to parameters. The CATSurface::GetParam method computes (if possible) the surface parameters of a given Cartesian point, and details if the point really is on the surface or not, and if there are several solutions.

The surface is responsible for the mapping between the (X, Y, Z) Cartesian coordinates and the (U, V) parameters, so that no assumptions must be maid about this mapping, except for a few objects that have published their own parameterization.

[Top]

Equations

It is useful to retrieve the equations representing the surface, especially when you want to operate the geometry. You can retrieve these equations as CATMathFunctionXY instances, that are transient and created under request.

All surface modification changes the equations. Thus, it is necessary to precisely define the use of the geometry equations. There are 3 main methods for using equations.

• CATSurface::Lock(): Locks the geometric object before asking for its equation. This operation:
• Declares a reference on the object, so that it cannot be deleted anymore.
• Increments the number of customers that wants to prevent the object from future modifications, except the relimitation.
• Does not compute anything.
• CATSurface::GetEquation(): Asks for the equation. This operation:
• Throws an exception if the object is not locked.
• Allocate the memory (if needed).
• Computes the equations (if needed).
• Returns a constant pointer to the required equation.
• CATSurface::Unlock(): Unlocks the geometric object when you do not need to use its equation no more. This operation:
• Releases the reference
• Decrements the number of customers which want to prevent the object from future modifications, except the relimitation.
• Keeps the allocated memory and computed equations as long as the object is not modified.

In case of a modification of a surface,

• If there remains at least one lock on the surface, an error is thrown
• Otherwise, the memory is freed.

[Top]

Various Types of Surfaces

You find four major surface types in the CGM offering: the resolved surfaces, the sampled surfaces, the multi-represented surfaces and the procedural surfaces.You can also introduce your own class of surface, and use it as any CGM surface in all the CGM operators or as the underlying geometry of a topological object. For a detailed description of this mechanism, see [2].

[Top]

Resolved Surfaces

These surfaces are only available on a mathematical form: NURBS, canonical surface (plane, cone, sphere, cylinder, torus) belongs to this type. Evaluations are made directly from the mathematical equations. The following array describes, for each resolved surface, its definition parameters, and the validity range of the definition parameters which come in addition to general validity criteria that have already been described.

[Top]

Sampled Surfaces

These surfaces result from a computation that does not lead to a canonical form. For example, a fillet with variable radius cannot be expressed in terms of a cylinder or another canonical surface. Moreover, the limiting curves in this case are defined by a Spline interpolation between marching points, obtained by a progressive algorithm. It is the reason why this type of surface is called sampled surface. For example, the CATGenericFilletSurface interface manages the behavior of a fillet surface that is not canonical, while the CATGenericRuledSurface interface manages the behavior of a draft surface that is not canonical.

[Top]

Multi-represented Surfaces

The multi-represented surface simply delegates, without computation, its evaluation to a pointed surface.This model allows CGM to keep as long as possible the object canonicity: for example, an object implementing the CATFilletSurface interface point to an objet implementing a canonical surface (such as CATCylinder, CATCone) or to an object implementing the CATGenericFillet if the resulting fillet is not canonical. The canonical representation, if it exists, is returned by the CATSurface::GetGeometricRep method.

Fig. 3: The multi-represented surfaces

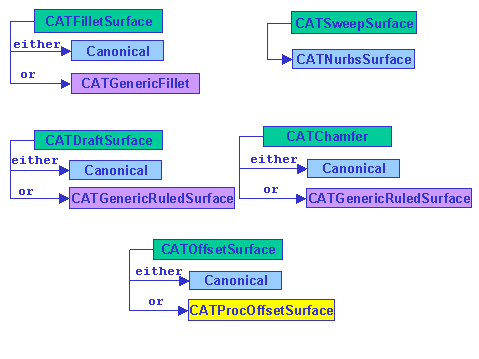CATFilletSurface, CATDraftSurface, CATSweepSurface, CATOffsetSurface are interfaces for various multi-represented surfaces. Each of these surface refers to another one for the evaluation process. The referred surface is preferably a canonical surface. If it is not possible, sampled or procedural surfaces are chosen.

Multi-represented surfaces are often created with geometric operators that are dedicated to this creation. The following array displays the geometric operator or the method of the CATGeoFactory to use for the creation of each type of multi-represented surface:

[Top]

Procedural Surfaces

The procedural surface uses the evaluation of another surface, call the reference, for the computation of its own evaluation. The reference can be any type of surface, even a procedural one. But in this last case, this will be more time consuming: two evaluations are done, one for each level. In case of a CATProcOffsetSurface referring another CATProcOffsetSurface however, the offset values are directly cumulated at the surface creation, so that only one evaluation is done.

Fig. 4: The evaluation mechanism and the special case of procedural offset surface

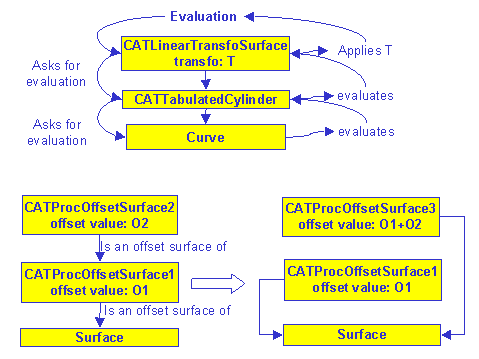When you ask for an evaluation of a procedural surface, the procedural surface uses the evaluation of its reference. This process is recursive if the reference is a procedural surface itself, so that it could be time consuming, because each procedural surface do computations at each level. This is not the case for a procedural offset surface of another procedural offset surface: here, the offset are cumulated, eliminating the recursivity.

We detail now the various procedural surfaces.

[Top]

In Short

• CGM surfaces are C2 continuous. They offer you evaluators to evaluate point parameters and derivatives, and equations to use in geometric operations for example.
• Four major types of surfaces are available: resolved surfaces, sampled surfaces, multi-represented surfaces and procedural surfaces. Foreign surfaces can also be introduced in CGM.

[Top]

References

History

Copyright © 2000, Dassault Systèmes. All rights reserved.