How are element stresses computed?
Element stresses at Gauss points are the product of the Comportment Law and the Strain Deformation.
|
|
-
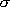is the element stress -
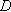is the Comportment Law, computed as a function of the following
parameters, where:-
is the Poisson Ratio -
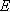is the Young's Modulus
-
-
is the Strain deformation, computed according to the displacement.For example, with a 2D displacement:
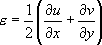
where
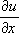and
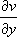are the two partial derivatives.
How are contact elements computed?
-
It is assumed that contact property is non-linear (of the form K.X = F(X) ). Nevertheless, in the particular case of contact without friction, the solution is unique: it does not depend of the path used to put the two geometries in contact.
Static solutions inside the Generative Part Structural Analysis (GPS) product are thus solved with an iterative algorithm which could be qualified by an "advanced linear" approach. At each computation step, local contact directions are not updated (contrary to non-linear solvers). But if the local curvature is small (compared to contact area width), this approximation remains reliable and gives good results.
The contact connection mesh is done between overlapping surfaces at their initial position. The solver does not take into account large relative sliding between surfaces in contact. Contact condition is only valid for elements connected by the mesh part.
-
To solve contact problems, an additional stiffness is added to the contact element.
Adding stiffness may influence displacements, especially in the case of two solids that are not really in contact.
For example: consider two surfaces (S1 and S2) with 2mm distance between.
Enforced displacements (dS1) are applied to S1: dS1 = -0.5mm.-
Case 1: (without contact)
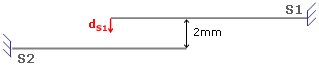
In this case, the displacement of the S2 surface are dS2 = 0mm.
-
Case 2: (with contact)
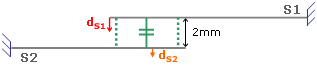
where
symbolizes the contact elements.In this case dS2 is not equal to zero but the displacements are very small.
-
How are node stresses computed?
Node stresses are extrapolations of element stresses.
The method consists in defining a continuous stress field within the element:
|
where:
|
These nodal stresses values are obtained using the least square minimization method:
|
where
|
How is error computed?
There are two steps in the error computation:
-
Stress smoothing.
This method consists in computing a weighted nodal stress value at each nodes.
For more information about the nodal stresses values, refer to How are computed node stresses?
-
Error estimation.
Once the nodal stresses values have been found, a continuous stress field is defined for each element:
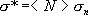
where:
-
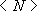are the element shape functions -
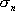are the smoothed nodal stresses
For more information about the nodal stresses values, refer to How are computed node stresses?
The error for each element (local error) is:
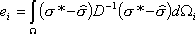
where:
-
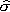is the finite element solution field -
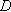is the Comportment Law
For more information about the nodal Comportment Law, refer to How are computed element stresses?
The total error (Estimated Precision) is the sum of all the local errors:
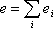
And the Global Estimated Error Rate is:
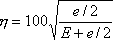
where
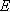is the global strain energy. -
How are result and computation files managed?
You can manage analysis results (contained in .CATAnalysisResults files) and analysis computations (contained in .CATAnalysisComputations files):
-
Specify the path of an external storage file directory.
For more details, refer to Specify External Storage. -
Clear Elfini Storage in order to save space on your disk.
For more details, refer to Clear External Storage. -
Specify a temporary data directory for the CATElfini stored data and computation results.
For more details, refer to Specify Temporary Data Directory.
You can also customize analysis default external storage
(computation and result data) settings.
For more details, refer to
External Storage.