Geometric Modeler
|
Topology
|
The Boolean Operators
Best Practices |
| Technical Article |
Abstract
The Boolean operators are the base operations of a topological modeler:
they allow the user to add, subtract or intersect topological objects,
called bodies. They are very sensitive to the geometry of overlapping
areas, that is, the place where the skins of the two objects are the same
or nearly the same. This article presents best practices to handle the
overlapping areas, in order to optimize the use of the Boolean operators.
|
Basic Boolean Operators
The Boolean operators add, subtract or intersect topological objects (called
bodies, see [1]). Moreover, these basic operations can
be combined to perform more complex one such a split, sewing or trim.
The Boolean operators proceed in three steps:
- Compute the intersection paths between all the boundaries of one body and
the boundaries of the other body. This splits each body into parts that
belong to only one body, or to the both;
- Assign an attribute of "Keep" or "Remove" to each
part, according to the operation;
- Build the resulting body.
Fig. 1: The Difference Operator
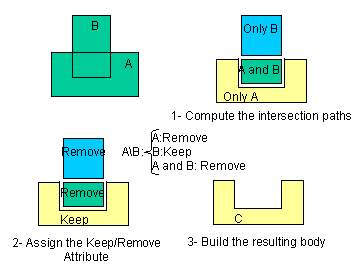 |
Fig. 1 illustrates the way Boolean
operators proceed, by taking the example of the difference operator.
The specificity of each operator are taken into account during the
second step:
- Difference or Subtract operator: the matter of B is
subtract from A. The parts only belonging to A are kept
- Union operator: the parts belonging to A, or to B,
or both, are kept
- Intersection operator: the parts common to both A
and B are kept.
|
When parts (such as "A and B" in Fig. 1),
common to both input bodies, have to be kept, they are "simplified":
they are taken as a single part in the final result.
The basic Boolean operators are exposed through the CATDynBoolean
class.
[Top]
Overlapping Configurations
The Boolean operators perform intersections to compute the paths, and then
split the input bodies into different parts. When the intersections between the
two bodies are frank, the operator is easily executed: it finds a point, if two
edges are intersected, an edge if two faces are intersected, or a face if two
volumes are intersected.
But imagine now that the two bodies have part of their boundaries that are
geometrically confused. In this case, the intersection may give an edge when
intersecting two edges, or a face when intersecting two faces.
These case are sensitive: they slow down the execution, and may lead to
results of lesser quality: creation of small numerous elements, as an example.
Fig. 2 depicts some overlapping cases.
Fig. 2: Overlapping situations
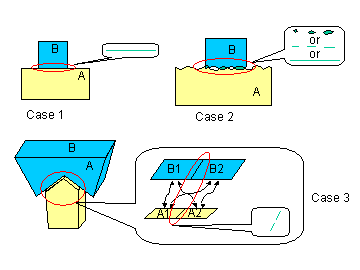 |
- Case1: the geometry is the same: either the topology refers
the same underlying geometry (most favorable case), or the geometry
type (such as plane) is the same and the parameters too.
- Case2: The geometry is the same, but was computed with an
interpolation between a list of points. In this case, the intersection
may lead to numerous small elements
- Case 3: The first step of a Boolean operator computes the
intersections between all the boundaries of one body and all the
boundaries of the other one. Here, are computed the intersections
between A1 and B1, A2 and B2, but also intersections between A1 and
B2, A2 and B1 leading to a patchwork of overlapping areas, and
increasing the risk to create small elements.
|
But the overlapping areas can be often avoided, by following some rules that
are described in the next section.
[Top]
Methodology
Some simple rules can help you to optimize your use of the Boolean operators:
- Use another object for the same result
- Match the faces of the two bodies that you know they are on the same
geometry
- Share geometric elements as much as possible
- Use Boolean operators that process several operation in one execution.
[Top]
Use a Different
Object for the Same Result
The idea is to change the shape of one of the operands (or both) to suppress
the overlapping, without changing the final result.
Fig. 3: Use a different object for the same
result
 |
In the first example, operating with a bigger B object leads to
suppress the overlap.
In the second example, B is taken smaller to suppress the overlap.
In the last example, a bigger B again leads to suppress the overlap. |
[Top]
Share Geometric
Elements as Much as Possible
A geometric element is shared if several cells directly refer it. In this
case the intersections between the cells referring the same geometric element
are not run and the overlap is treated as a logical information.
A logical information can also be put directly by specialized operators, that
precisely know the build of their object. It is the goal of the next section.
[Top]
Match the Faces
If you write your own operator, match the cells that you know they will refer
the same geometry. The matching can be down by the means of transient
attributes, see [2] to learn how to use them.
Fig. 4: The shell operator uses attributes to
avoid computation of overlapping areas
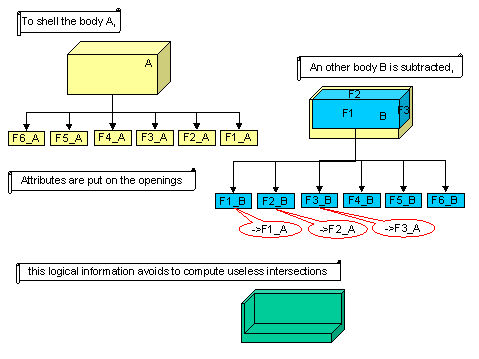 |
The principle of the shell operator is to create a new body
by digging matter inside an initial body: a thickness is given for each
face. If the thickness is null, the face is an opening, leading to a
overlapping area. There are three openings in the beside figure.
Now, the shell operator exactly knows that F1_B and F1_A, F2_B and
F2_A, F3_B and F3_A respectively match, and put attributes to keep this
logical information.
Hence, the intersection between the geometry of these faces are not
run, but directly determined. |
[Top]
Process Several
Boolean Operations in One Shot
The idea is to use operator of higher level, instead of chaining several
basic Boolean operators, and creating overlap situations.
[Top]
Split Operator
The split operator removes matter that is on a given side of the object to
split.
The split operator offers you two versions, according to the type of object
you want to split:
- To split a volume by a skin, use the CATDynSplit class
- To split a shell by a wire, or a wire by a vertex, use the CATHybOperator
class, which instances are created by the CreateHybSplit global
function.
Both ask for the side on each operand, on which the matter has to be kept.
Fig. 5: Splitting a Volume by a Surface
 |
Take for example the split of the light blue Pad by the
orange Surface. |
 |
The intersection between the Pad and the Surface lets marks
on both objects. In the case of the beside figure, the Split operator
removes the matter of the Pad that is upside the Surface (the surface
itself is hidden to better show the result). |
 |
On the contrary, the Split operator removes here the matter
of the Pad that is below the Surface (The surface itself is again hidden
to better show the result). |
[Top]
Sewing Operator
Sewing means joining together a surface and a body. This capability consists
in computing the intersection between a given surface and a body while removing
useless material (such as a split operation). Moreover, material is added to the
body if the intersection paths define closed contours. This operator is managed
by the CATSewing class.
Fig. 6: Sewing a Surface on a Body.
 |
Take the example of Fig. 5, that is
again displayed besides. |
 |
The Pad material that is upside the Surface is removed.
Moreover, the intersection path on the upper face is closed. So that the
dome is that is defined by this way is added to the initial Pad.
Notice that in this case, choosing to remove the matter that is below
the Surface does not lead to a correct result: it would twist the
resulting body. |
[Top]
Trim Operator
The Trim operation is a way to shrewdly tune the parts to be kept or removed
after the computation of the intersection paths. Three majors rules govern this
operator:
- If at least one face is stamped "keep", all the volumes that do
not have faces stamped "keep" are removed
- A volume which one face is stamped "remove" is removed.
The "keep" and "remove" stamps can be put on both input
bodies, but must be consistent. The common parts are always kept.
Fig. 7 The rules of the Trim operator
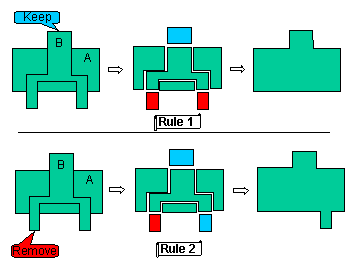 |
- Rule 1
The top face of Body B is stamped "keep". All the volumes of
this body that do not own this face are removed, except the common
parts between Body A and Body B. As nothing is said about Body A, all
its volumes are kept.
- Rule 2
A bottom face of body B is stamped "remove". All is kept
except the volume that owns this face.
|
There are two classes to handle the trim operation:
- To trim two volumes, use the CATTopologicalOperator::Trim method.
- To trim two shells, or two wires, use the CATHybOperator class,
which instances are created by the CreateHybTrim global function.
[Top]
Use a Logical Way to
Describe Primitives
Some primitives such as Pad or Revolute are defined as the extrusion or
rotation of a contour. You can define the height of a Pad by giving a numerical
number or by defining it logically: the Pad ends as it encounters a given
surface. In this last case, the operator that creates the Pad (CATTopPrism)
uses the logical information and does not compute useless intersections.
Moreover, it allows you to directly chain the Boolean operation in a single
execution (SetBooleanResult method).
Fig. 8 : Definition of a Pad "Until"
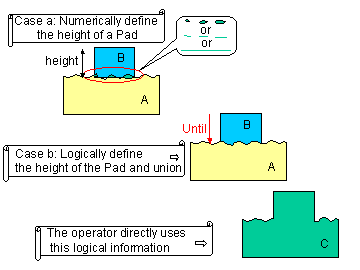 |
The Case "b" is a better way to proceed: it allows
you to give a logical information to the prism operator, that is used to
avoid useless computations. |
[Top]
In Short
- The Boolean operators are basic topological tools to add and subtract
matter. They are very sensitive to overlapping areas of the boundaries of
the input bodies, and these situations must be avoided.
- Some simples rules can help you to get rid of overlaps, by modifying
operands, using logical information or operators that process several
operations in one shot, such as the split, the sewing or the trim operator.
[Top]
References
History
| Version: 1 [Mar 2000] |
Document created |
| [Top] |
Copyright © 2000, Dassault Systèmes. All rights reserved.









