Geometric Modeler

Introduction

The topology is a building set for limiting the space. Vertex bound edges, which bound faces, which bound volumes. How to map these topological entities to geometric entities in order to limit the geometric space?

• a CATMacroPoint corresponds to the geometric support of a vertex,
• a CATEdgeCurve corresponds to the geometric support of an edge,
• a CATSurface corresponds to the geometric support of a face.

[Top]

Representing Geometry

A CATEdgeCurve Represents CATCurves

Consider the intersection curve of two surfaces. From the topological point of view, its geometry is represented by a CATEdgeCurve. From a geometric point of view, this curve may be seen as a curve on the first surface or as a curve on the second surface.

Hence, a CATEdgeCurve is the geometric representation of the topological edge, which may be seen under several representations.

When the curve is not the result of an intersection, the CATEdgeCurve may contain CATCurves that are not CATPCurves.

[Top]

A CATMacroPoint Represents CATPoints

Consider now the intersection point of two CATEdgeCurves. From the topological point of view, its geometry is represented by a CATMacroPoint. From a geometric point of view, this point may be seen as a point on the first edge curve (called CATPointOnEdgeCurve or POEC) or as a POEC on the second edge curve.

Hence, a CATMacroPoint is the geometric representation of the topological vertex, which may be seen under several representations.

When the curve is not the result of an intersection, the CATMacroPoint may contain CATPoints that are not CATPointOnEdgeCurves.

[Top]

The Cell Geometry Depends on What It Bounds

Here is detailed the precise rules of the geometry-topology relations, according to the type of domains that a cell bounds.

What Is Related to a Volume

The geometric entity corresponding to a volume is the whole space, which is the same for all volumes. It is the reason why we do not have to precise it.

What Is Related to a Face

The geometric entity corresponding to a face is a CATSurface.

What Is Related to an Edge

The geometric entity corresponding to an edge is a CATEdgeCurve. Imagine you want to use this CATEdgeCurve as geometry for the topology. Depending on how the edge is used to border (or not) a cell of higher dimension, the CATEdgeCurve will represent different types of curve.

• The edge will only border a face: the edge curve represents (at least) a CATPCurve.
• The edge will border several faces: the edge curve represents (at least) as many CATPCurves as there are faces bounded by this edge.
• The edge belongs to a CATWire: the edge curve represents any type of CATCurves.

[Top]

What Is Related to a Vertex

The geometric entity corresponding to a vertex is a CATMacroPoint. Imagine you want to use this CATMacroPoint as geometry for the topology. Depending on how the vertex is used to border (or not) a cell of higher dimension, this CATMacroPoint will represent different types of points.

• If the vertex will border an edge: the macro point represents (at least) a POEC corresponding to this limit of the edge.
• If the vertex will border several edges: the macro point represents (at least) as many POECs as there are edges bounded by this vertex.
• If the vertex will be drowned in a face (it will belong to a CATVertexInFace domain): the macro point represents (at least) a CATPointOnSurface. Note that for the moment, the CATVertexInFace also directly refers to the CATPointOnSurface, but this will be removed.
• If the vertex will be drowned in a volume (it will belong to a CATPointInVolume domain): the macro-point represents (at least) any type of CATPoints.

[Top]

Diagrams

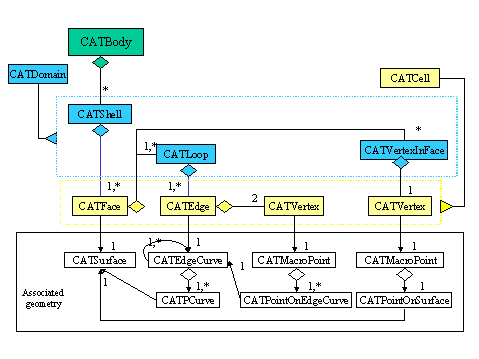
The following diagrams summarize the different configurations between the geometry and the topology.

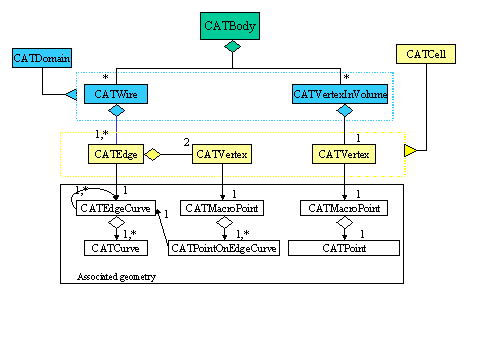Fig. 1: Geomery associated with topology: the case of the Shell domain

Fig. 2: Geomery associated with topology: the case of the Wire and VertexInVolume domain

[Top]

Main Steps to Create Cells Related to Geometry

We suppose in all these examples that a CATGeoFactory and a CATBody have been already created. These examples only detail the cell construction. You must then create the domain (Lump, Shell, Wire, VertexInVolume) containing the cells and add it to the body to complete it. For code examples, see.

[Top]

Main Steps to Create a Vertex

1. From a geometric point, eventually create a POEC or CATPointOnSurface, and relate it to a CATMacroPoint.
2. Create the CATVertex and associate it with the macro-point.

[Top]

Main Steps to Create an Edge

1. From a CATCurve, eventually create a CATPCurve, and relate it to a CATEdgeCurve.
2. Determine two parameters on the curve. Create the POECs and relate them to a CATMacroPoint.
3. Create the vertices (CATVertex) and associate them with their corresponding macro-points.
4. Create the edges, associate them with their CATEdgeCurves and border them with their vertices.

Note: A CATEdgeCurve cannot be directly created. Only its derived types (CATSimCurve, CATIntCurve, CATMergedCurve can be instantiated). For determining the choice of one of these objects, see About Edge Curves.

[Top]

Main Steps to Create a Face

1. Follows the steps of the preceding section to create the vertices and the edges. The edges must be associated with CATEdgeCurves containing CATPCurves.
2. Create a CATLoop.
3. Create a CATFace, associate it with its CATSurface and border it by the edges, building up the loop.

[Top]

Main Steps to Create a Volume

1. Follows the steps of the preceding section to create the vertices, edges and faces.
2. Create a CATShell.
3. Create a CATVolume and border it by the faces, building up the shell.

[Top]

Example: Wire Creation

This section details step by step the creation of a Wire containing one edge.

1. Geometry Creation

CATCartesianPoint * Point1=factory->CreateCartesianPoint(0,0,0);
CATCartesianPoint * Point2=factory->CreateCartesianPoint(0,10,0);
CATLine *           Line  =factory->CreateLine(Point1,Point2);      

2. CATEdgeCurve Creation

CATSimCurve *           SimCurve  =factory->CreateSimCurve(Line);

3. CATPointOnEdgeCurve and CATMacroPoint Creation

CATCrvParam       Param
CATCrvLimit       Limit = Line->GetLimits;
Limit.GetLow(Param);
CATPointOnEdgeCurve *
                   Poec1 = factory->CreatePointOnEdgeCurve(Line,Param,SimCurve);
Limit.GetHigh(Param);
CATPointOnEdgeCurve *
                   Poec2 = factory->CreatePointOnEdgeCurve(Line,Param,SimCurve);
CATMacroPoint      Macro1= factory->CreateMacroPoint();
Macro1->Append(Poec1);
CATMacroPoint      Macro2= factory->CreateMacroPoint();
Macro2->Append(Poec2);

4. Vertex Creation; Association with the Geometry

CATVertex * Vertex1=body->CreateVertex();
Vertex1->SetGeometry(Macro1);
CATVertex * Vertex2=body->CreateVertex();
Vertex2->SetGeometry(Macro2);

5. CATEdge Creation, Association with the Geometry, Boundary Definition.

CATEdge *   Edge= body->CreateEdge();
Edge->SetCurve(SimCurve);
Edge->AddBoundingCell(Vertex1,CATSideLeft,NULL,Poec1);
Edge->AddBoundingCell(Vertex2,CATSideLeft,NULL,Poec2);

6. Wire Creation.

CATWire Wire=body->CreateWire();

7. Append the Edge into the Wire.

Wire->AddCell(Edge);

8. Append the Wire into the Body.

Body->AddDomain(Wire);

Note: This was detailed for explaining all the capabilities of the topological objects. You can use operators such as CATWireOperator or CATSkinOperator to directly create domains from geometry.

[Top]

In Short

• A CATMacroPoint is the geometry of a CATVertex. It can represent different types of points depending on what type of domains it bounds. In peculiar, a CATVertex bounding a CATEdge  is related to a CATMacroPoint representing a CATPointOnEdgeCurve.
• A CATEdgeCurve is the geometry of a CATEdge. It can represent different types of curves depending on what type of domains it bounds. In peculiar, a CATEdge bounding a CATFace (resp. CATWire) is related to a CATEdgeCurve representing a CATPCurve (resp. CATCurve).
• Topological operators allow you to easily create domains.

[Top]

References

History

Copyright © 2000, Dassault Systèmes. All rights reserved.