Failure Criteria

This task gives you detailed formulas of failure criteria you can visualize as post-processing results using the Generate Image command:

• Failure Criteria for Composite Properties
• Failure Criteria for Isotropic Materials.

Failure Criteria for Composite Properties

If you are in a composite context and the material you refer to is orthotropic (Orthotropic material 2D, Orthotropic material 3D and Fiber material), you can compute failure criteria and visualize them as post-processing results. Those failure criteria are Tsai-Hill, Tsai-Wu, Maximum Failure and Hoffman.

You can define the characteristics of orthotropic materials in the Analysis tab of the Properties dialog box. To know more about this dialog box, refer to Modifying Material Physical Properties.

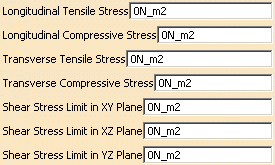
• Longitudinal Tensile Stress corresponds to the ultimate stress in tension along the X direction (S_1T).
• Longitudinal Compressive Stress corresponds to the ultimate stress in compression along the X direction (S_1C).
• Transverse Tensile Stress corresponds to the ultimate stress in tension along the Y direction (S_2T).
• Transverse Compressive Stress corresponds to the ultimate stress in compression along the Y direction (S_2C).
• Shear Stress Limit in XY Plane corresponds to the ultimate shear stress in the XY-plane (S₁₂).
• Shear Stress Limit in YZ Plane corresponds to the ultimate shear stress in the YZ-plane (S₂₃).
• Shear Stress Limit in XZ Plane corresponds to the ultimate shear stress in the XZ-plane (S₁₃).

Tsai-Hill Criterion

For each lamina the Tsai-Hill failure criterion requires that:

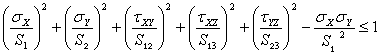
where:

• S₁ = S_1C if
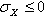
• S₁ = S_1T if
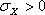
• S₂ = S_2C if
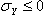
• S₂ = S_2T if

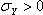
• For the 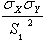term: if 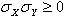, S₁ = S_1T; otherwise S₁ = S_1C

Tsai-Wu Criterion

For each lamina the Tsai-Wu failure criterion requires that:

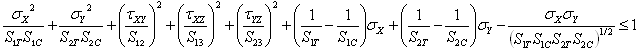
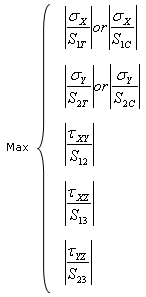
Maximum Failure Criterion

The maximum failure criterion is defined as follows:

Hoffman Criterion

The Hoffman criterion requires that:

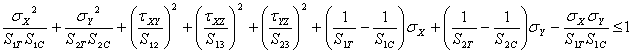
If one of the shear stress values (Shear Stress Limit in XY Plane, Shear Stress Limit in YZ Plane or Shear Stress Limit in XZ Plane) is not defined in the Properties dialog box, the associated term is neglected in the formula (S₁₂, S₂₃ and S₁₃ cannot be null in the formula).
For example: if you enter 0 as Shear Stress Limit in XY Plane value (S₁₂=0) in the Properties dialog box, the Tsai-Hill failure criteria requires that:

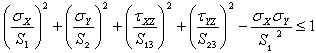
This means that the shear stresses in the XY-plane are neglected.
 

The formula are different depending on the:

• Material behavior (2D orthotropic, 3D orthotropic or fiber):
  • Fiber materials: the shear stress values in the YZ-plane and in the XZ-plane are equal (S₂₃ = S₁₃).
  • Orthotropic 2D materials: terms associated to the Z-plane are neglected in the Tsai-Hill and Tsai-Wu formulas.
  • Orthotropic 3D materials: all terms can be considered in the formulas.
• Finite element physical type:
  • Shell: all terms can be considered in the formulas.
  • Membrane: terms associated to the Z-plane are considered as null in the formulas.
  • Shear Panel: only shear effects in the XY-plane are taken into account in the formulas.

Failure Criteria for Isotropic Materials

If you work with an isotropic material, you can compute failure criteria and visualize them as post-processing results. Those criteria are Tresca, Tresca Stress and Von Mises.

Tresca Stress Criterion

The Tresca stress criterion is defined as follows:

where are the principal stresses.

Tresca Criterion

The Tresca criterion requires that:

where Re is the linear elastic limit.

Von Mises Criterion

The Von Mises criterion requires that:

where Re is the linear elastic limit.